Trong các bài viết trước của chúng tôi về Phân tích các thuật toán , chúng tôi đã thảo luận ngắn gọn về các ký hiệu tiệm cận, hiệu suất trường hợp xấu nhất và tốt nhất của chúng, v.v. Trong bài viết này, chúng tôi thảo luận về việc phân tích thuật toán sử dụng ký hiệu tiệm cận Big-O một cách chi tiết.
Phân tích thuật toán Big-O
Chúng ta có thể thể hiện độ phức tạp của thuật toán bằng cách sử dụng ký hiệu big-O. Đối với bài toán cỡ N:
- Một hàm / phương thức thời gian không đổi là “bậc 1”: O (1)
- Một hàm / phương pháp thời gian tuyến tính là “bậc N”: O (N)
- Một hàm / thời gian bậc hai là "bậc N bình phương": O (N 2)
Định nghĩa: Cho g và f là các hàm từ tập hợp các số tự nhiên đến chính nó. Hàm f được cho là O (g) (đọc là big-oh của g), nếu tồn tại một hằng số c> 0 và một số tự nhiên n 0 sao cho f (n) ≤ cg (n) với mọi n> = n 0 .
Lưu ý: O (g) là một tập hợp!
Lạm dụng ký hiệu: f = O (g) không có nghĩa là f ∈ O (g).
Kí hiệu tiệm cận Big-O cung cấp cho chúng ta Ý tưởng Giới hạn Trên, được mô tả về mặt toán học dưới đây:
f (n) = O (g (n)) nếu tồn tại một số nguyên dương n 0 và một hằng số dương c, sao cho f (n) ≤cg (n) ∀ n≥n 0
Quy trình chung bước khôn ngoan để phân tích thời gian chạy Big-O như sau:
- Tìm ra đầu vào là gì và n đại diện cho cái gì.
- Biểu thị số hoạt động tối đa, thuật toán thực hiện theo n.
- Loại bỏ tất cả ngoại trừ các điều khoản đặt hàng cao nhất.
- Loại bỏ tất cả các yếu tố không đổi.
Một số thuộc tính hữu ích của phân tích ký hiệu Big-O như sau:
Phép nhân Hằng số:
Nếu f (n) = cg (n), thì O (f (n)) = O (g (n)); trong đó c là một hằng số khác không.
Hàm đa thức:
Nếu f (n) = a 0 + a 1 .n + a 2 .n 2 + —- + a m .n m thì O (f (n)) = O (n m ).
Hàm tính tổng:
Nếu f (n) = f 1 (n) + f 2 (n) + —- + f m (n) và f i (n) ≤f i + 1 (n) ∀ i = 1, 2, —-, m,
thì O (f (n)) = O (max (f 1 (n), f 2 (n), —-, f m (n))).
Hàm logarit:
Nếu f (n) = log a n và g (n) = log b n thì O (f (n)) = O (g (n))
; tất cả các chức năng nhật ký phát triển theo cùng một cách thức đối với Big-O.
Về cơ bản, ký hiệu tiệm cận này được sử dụng để đo lường và so sánh các trường hợp xấu nhất của các thuật toán về mặt lý thuyết. Đối với bất kỳ thuật toán nào, phân tích Big-O nên đơn giản miễn là chúng ta xác định chính xác các hoạt động phụ thuộc vào n, kích thước đầu vào.
Phân tích thời gian chạy của các thuật toán
Trong các trường hợp chung, chúng tôi chủ yếu sử dụng để đo lường và so sánh độ phức tạp thời gian chạy lý thuyết trong trường hợp xấu nhất của các thuật toán để phân tích hiệu suất.
Thời gian chạy nhanh nhất có thể cho bất kỳ thuật toán nào là O (1), thường được gọi là Thời gian chạy không đổi . Trong trường hợp này, thuật toán luôn mất cùng một khoảng thời gian để thực thi, bất kể kích thước đầu vào là bao nhiêu. Đây là thời gian chạy lý tưởng cho một thuật toán, nhưng hiếm khi có thể đạt được.
Trong trường hợp thực tế, hiệu suất (Runtime) của một thuật toán phụ thuộc vào n, đó là kích thước của đầu vào hoặc số lượng hoạt động được yêu cầu cho mỗi mục đầu vào.
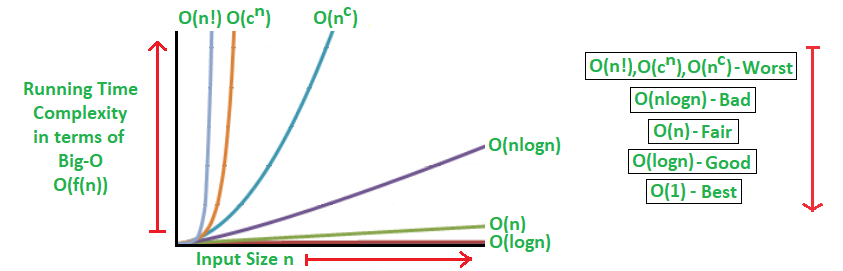
Các thuật toán có thể được phân loại như sau từ hiệu suất tốt nhất đến kém nhất (Độ phức tạp thời gian chạy):
Một thuật toán logarit - O (logn)
Thời gian chạy tăng theo logarit theo tỷ lệ với n.
Thuật toán tuyến tính - O (n)
Thời gian chạy tăng trực tiếp theo tỷ lệ với n.
Một thuật toán siêu tuyến tính - O (nlogn)
Thời gian chạy tăng tỷ lệ với n.
Một thuật toán đa thức - O (n c )
Thời gian chạy phát triển nhanh hơn tất cả dựa trên n.
Thuật toán hàm mũ - O (c n )
Thời gian chạy thậm chí còn phát triển nhanh hơn thuật toán đa thức dựa trên n.
Một thuật toán giai thừa -
Thời gian chạy O (n!) Phát triển nhanh nhất và nhanh chóng trở nên không sử dụng được đối với
các giá trị thậm chí nhỏ của n.
Trong đó, n là kích thước đầu vào và c là hằng số dương.
Ví dụ thuật toán về phân tích thời gian chạy :
Một số ví dụ về tất cả các loại thuật toán đó (trong trường hợp xấu nhất) được đề cập dưới đây:
Thuật toán lôgarit - O (logn) - Tìm kiếm nhị phân.
Thuật toán tuyến tính - O (n) - Tìm kiếm tuyến tính.
Thuật toán siêu tuyến - O (nlogn) - Sắp xếp đống, Sắp xếp hợp nhất.
Thuật toán đa thức - O (n ^ c) - Phép nhân ma trận Strassen, Sắp xếp bong bóng, Sắp xếp lựa chọn, Sắp xếp chèn, Sắp xếp theo nhóm.
Thuật toán hàm mũ - O (c ^ n) - Tháp Hà Nội.
Thuật toán giai thừa - O (n!) - Mở rộng Định thức theo Trẻ vị thành niên, Thuật toán tìm kiếm bạo lực cho Bài toán Người bán hàng Đi du lịch.
Ví dụ toán học về phân tích thời gian chạy :
Các hiệu suất ( Thời gian chạy ) của các thứ tự thuật toán khác nhau tách biệt nhanh chóng khi n (kích thước đầu vào) lớn hơn. Hãy xem xét ví dụ toán học:
Nếu n = 10, Nếu n = 20, log (10) = 1; log (20) = 2,996; 10 = 10; 20 = 20; 10log (10) = 10; 20log (20) = 59,9; 102=100; 202=400; 210=1024; 220=1048576; 10! = 3628800; 20! = 2.432902e + 18 18 ;
Phân tích dấu chân bộ nhớ của các thuật toán
Để phân tích hiệu suất của một thuật toán, phép đo thời gian chạy không chỉ là số liệu liên quan mà chúng ta cần xem xét dung lượng sử dụng bộ nhớ của chương trình. Đây được gọi là Dấu chân bộ nhớ của thuật toán, được gọi ngắn gọn là Độ phức tạp không gian.
Ở đây, chúng ta cũng cần đo lường và so sánh các trường hợp xấu nhất về độ phức tạp không gian lý thuyết của các thuật toán để phân tích hiệu suất.
Về cơ bản, nó phụ thuộc vào hai khía cạnh chính được mô tả dưới đây:
- Thứ nhất, việc thực hiện chương trình chịu trách nhiệm về việc sử dụng bộ nhớ. Ví dụ, chúng ta có thể giả định rằng việc triển khai đệ quy luôn dự trữ nhiều bộ nhớ hơn so với việc thực hiện lặp đi lặp lại tương ứng của một vấn đề cụ thể.
- Và cái còn lại là n, kích thước đầu vào hoặc số lượng lưu trữ cần thiết cho mỗi mặt hàng. Ví dụ: một thuật toán đơn giản với số lượng kích thước đầu vào cao có thể tiêu tốn nhiều bộ nhớ hơn một thuật toán phức tạp với lượng kích thước đầu vào ít hơn.
Ví dụ thuật toán về phân tích dấu chân bộ nhớ: Các thuật toán với các ví dụ được phân loại từ hiệu suất tốt nhất đến kém nhất (Độ phức tạp về không gian) dựa trên các tình huống xấu nhất được đề cập bên dưới:
Thuật toán lý tưởng - O (1) - Tìm kiếm tuyến tính, Tìm kiếm nhị phân, Sắp xếp bong bóng, Sắp xếp lựa chọn, Sắp xếp chèn, Sắp xếp đống, Sắp xếp Shell.
Đánh đổi không gian-thời gian và hiệu quả
Thường có sự đánh đổi giữa việc sử dụng bộ nhớ tối ưu và hiệu suất thời gian chạy.
Nói chung đối với một thuật toán, hiệu suất không gian và hiệu quả thời gian đạt đến ở hai đầu đối diện và mỗi điểm ở giữa chúng có một hiệu quả về thời gian và không gian nhất định. Vì vậy, bạn càng có nhiều hiệu quả về thời gian thì bạn càng có ít hiệu quả về không gian hơn và ngược lại.
Ví dụ: thuật toán Mergesort cực kỳ nhanh nhưng cần nhiều không gian để thực hiện các thao tác. Mặt khác, Bubble Sort cực kỳ chậm nhưng yêu cầu không gian tối thiểu.
Ở phần cuối của chủ đề này, chúng ta có thể kết luận rằng việc tìm ra một thuật toán hoạt động trong thời gian chạy ít hơn và cũng có ít yêu cầu về dung lượng bộ nhớ hơn, có thể tạo ra sự khác biệt rất lớn về mức độ hoạt động của một thuật toán.
Đăng nhận xét