Bài đăng nổi bật
Giải thích về Kí hiệu Big O là gì: Sự phức tạp về không gian và thời gian
Nếu bạn đã thực hiện một số các khóa học thuật toán liên quan, có lẽ bạn đã nghe nói về thuật ngữ Big O ký hiệu . Nếu bạn chưa có, chúng ta sẽ xem xét nó ở đây, và sau đó hiểu sâu hơn về nó thực sự là gì.
Ký hiệu Big O là một trong những công cụ cơ bản nhất để các nhà khoa học máy tính phân tích chi phí của một thuật toán. Đó là một thực tiễn tốt cho các kỹ sư phần mềm để hiểu sâu hơn.
Bài viết này được viết với giả định rằng bạn đã giải quyết một số mã. Ngoài ra, một số tài liệu chuyên sâu cũng yêu cầu các nguyên tắc cơ bản về toán trung học phổ thông, và do đó có thể ít thoải mái hơn một chút đối với những người mới bắt đầu. Nhưng nếu bạn đã sẵn sàng, hãy bắt đầu!
Trong bài viết này, chúng ta sẽ thảo luận sâu hơn về ký hiệu Big O. Chúng tôi sẽ bắt đầu với một thuật toán ví dụ để mở rộng sự hiểu biết của chúng tôi. Sau đó, chúng ta sẽ đi sâu vào toán học một chút để có một sự hiểu biết chính thức. Sau đó, chúng ta sẽ xem xét một số biến thể phổ biến của ký hiệu Big O. Cuối cùng, chúng ta sẽ thảo luận về một số hạn chế của Big O trong một kịch bản thực tế. Mục lục có thể được tìm thấy bên dưới.
Mục lục
- Ký hiệu Big O là gì và tại sao nó lại quan trọng
- Định nghĩa chính thức của ký hiệu Big O
- Big O, Little O, Omega & Theta
- So sánh độ phức tạp giữa các Big Os điển hình
- Thời gian & Không gian phức tạp
- Tốt nhất, Trung bình, Tồi tệ nhất, Độ phức tạp Dự kiến
- Tại sao Big O không quan trọng
- Đến cuối cùng…
Vậy hãy bắt đầu.
1. Ký hiệu Big O là gì, và tại sao nó lại quan trọng
“Ký hiệu Big O là một ký hiệu toán học mô tả hành vi giới hạn của một hàm khi đối số có xu hướng hướng tới một giá trị cụ thể hoặc vô cùng. Nó là một thành viên của nhóm ký hiệu do Paul Bachmann, Edmund Landau và những người khác phát minh, được gọi chung là ký hiệu Bachmann – Landau hoặc ký hiệu tiệm cận. ”
- Định nghĩa của Wikipedia về ký hiệu Big O
Nói một cách dễ hiểu, ký hiệu Big O mô tả độ phức tạp của mã của bạn bằng cách sử dụng các thuật ngữ đại số.
Để hiểu ký hiệu Big O là gì, chúng ta có thể xem một ví dụ điển hình, O (n²) , thường được phát âm là “Big O bình phương” . Chữ cái “n” ở đây đại diện cho kích thước đầu vào và hàm “g (n) = n²” bên trong “O ()” cho chúng ta ý tưởng về mức độ phức tạp của thuật toán đối với kích thước đầu vào.
Một thuật toán điển hình có độ phức tạp là O (n²) sẽ là thuật toán sắp xếp lựa chọn . Sắp xếp lựa chọn là một thuật toán sắp xếp lặp qua danh sách để đảm bảo mọi phần tử tại chỉ mục i là phần tử nhỏ nhất / lớn nhất thứ i của danh sách. Các CODEPEN dưới đây đưa ra một ví dụ trực quan của nó.
Thuật toán có thể được mô tả bằng đoạn mã sau. Để đảm bảo phần tử thứ i là phần tử nhỏ nhất thứ i trong danh sách, thuật toán này trước tiên sẽ lặp qua danh sách bằng một vòng lặp for. Sau đó, đối với mỗi phần tử, nó sử dụng một vòng lặp for khác để tìm phần tử nhỏ nhất trong phần còn lại của danh sách.
SelectionSort(List) {
for(i from 0 to List.Length) {
SmallestElement = List[i]
for(j from i to List.Length) {
if(SmallestElement > List[j]) {
SmallestElement = List[j]
}
}
Swap(List[i], SmallestElement)
}
}Trong trường hợp này, chúng tôi coi biến Danh sách là đầu vào, do đó kích thước đầu vào n là số phần tử bên trong Danh sách . Giả sử câu lệnh if và phép gán giá trị bị ràng buộc bởi câu lệnh if, mất thời gian không đổi. Sau đó, chúng ta có thể tìm thấy ký hiệu O lớn cho hàm SelectionSort bằng cách phân tích số lần các câu lệnh được thực thi.
Đầu tiên, vòng lặp for bên trong chạy các câu lệnh bên trong n lần. Và sau khi tôi được tăng lên, vòng lặp for bên trong chạy trong n-1 lần…… cho đến khi nó chạy một lần, sau đó cả hai vòng lặp for đều đạt đến điều kiện kết thúc của chúng.
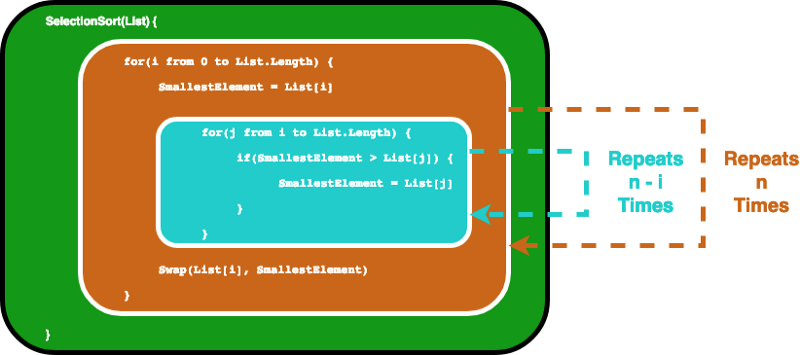
Điều này thực sự kết thúc cho chúng ta một tổng hình học và với một số môn toán trung học, chúng ta sẽ thấy rằng vòng lặp bên trong sẽ lặp lại 1 + 2… + n lần, tương đương với n (n-1) / 2 lần. Nếu chúng ta nhân số này với nhau, chúng ta sẽ nhận được n² / 2-n / 2.
Khi chúng ta tính toán ký hiệu O lớn, chúng ta chỉ quan tâm đến các số hạng chi phối , và chúng ta không quan tâm đến các hệ số. Vì vậy, chúng tôi lấy n² là chữ O. Lớn cuối cùng của chúng tôi. Chúng tôi viết nó là O (n²), một lần nữa được phát âm là “Big O bình phương” .
Bây giờ bạn có thể tự hỏi, "thuật ngữ thống trị" này là về cái gì? Và tại sao chúng ta không quan tâm đến các hệ số? Đừng lo lắng, chúng tôi sẽ điểm qua từng cái một. Có thể hơi khó hiểu ở phần đầu, nhưng tất cả sẽ có ý nghĩa hơn khi bạn đọc qua phần tiếp theo.
2. Định nghĩa chính thức của ký hiệu Big O
Ngày xưa, có một vị vua Ấn Độ muốn ban thưởng cho một nhà thông thái vì sự xuất sắc của ông ta. Nhà thông thái không yêu cầu gì ngoài một ít lúa mì có thể lấp đầy bàn cờ.
Nhưng đây là quy tắc của anh ta: trong ô đầu tiên anh ta muốn 1 hạt lúa mì, sau đó là 2 ở ô thứ hai, rồi 4 ở ô tiếp theo… mỗi ô trên bàn cờ cần được lấp đầy bằng gấp đôi số hạt như trước. một. Vị vua ngây thơ đồng ý mà không do dự, nghĩ rằng đó sẽ là một yêu cầu tầm thường để đáp ứng, cho đến khi ông thực sự tiếp tục và thử nó…

Vậy nhà vua nợ nhà thông thái bao nhiêu hạt lúa mì? Chúng ta biết rằng một bàn cờ vua có 8 ô vuông bằng 8 ô vuông, tổng 64 ô vuông, vì vậy ô cuối cùng phải có 2⁶⁴ hạt lúa mì. Nếu bạn thực hiện một phép tính trực tuyến, bạn sẽ nhận được 1.8446744 * 10¹⁹, tức là khoảng 18, theo sau là 18 số 0. Giả sử rằng mỗi hạt lúa mì có trọng lượng 0,01 gam, điều đó cho chúng ta 184.467.440.737 tấn lúa mì. Và 184 tỷ tấn là khá nhiều phải không?
Các con số tăng trưởng khá nhanh sau đó để tăng trưởng theo cấp số nhân phải không? Logic tương tự cũng xảy ra đối với các thuật toán máy tính. Nếu những nỗ lực cần thiết để hoàn thành một nhiệm vụ tăng lên theo cấp số nhân đối với kích thước đầu vào, thì nó có thể trở nên cực kỳ lớn.
Bây giờ bình phương của 64 là 4096. Nếu bạn thêm số đó vào 2⁶⁴, nó sẽ bị mất bên ngoài các chữ số có nghĩa. Đây là lý do tại sao, khi chúng ta nhìn vào tốc độ tăng trưởng, chúng ta chỉ quan tâm đến các điều khoản chi phối. Và vì chúng tôi muốn phân tích sự tăng trưởng liên quan đến kích thước đầu vào, nên các hệ số chỉ nhân số thay vì tăng trưởng với kích thước đầu vào không chứa thông tin hữu ích.
Dưới đây là định nghĩa chính thức của Big O:
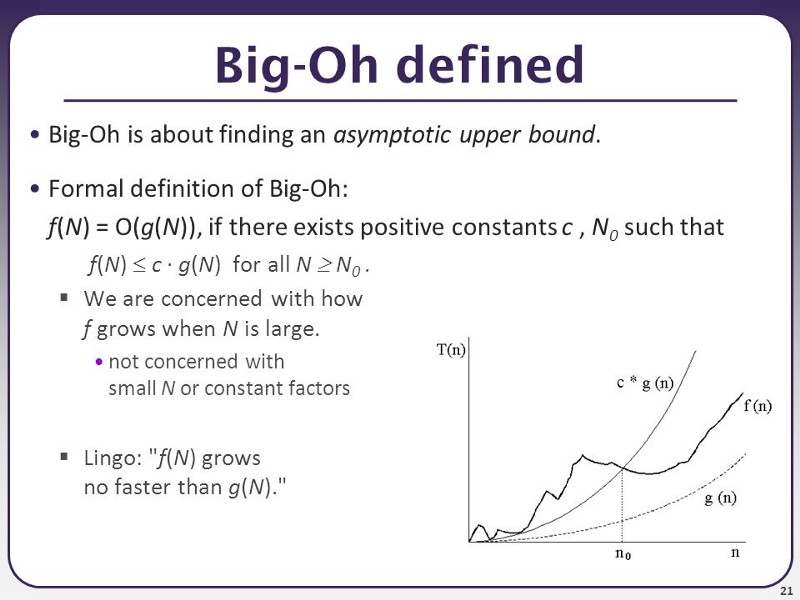
Định nghĩa hình thức rất hữu ích khi bạn cần thực hiện một phép toán. Ví dụ, độ phức tạp về thời gian để sắp xếp lựa chọn có thể được xác định bởi hàm f (n) = n² / 2-n / 2 như chúng ta đã thảo luận trong phần trước.
Nếu chúng ta cho phép hàm g (n) là n², chúng ta có thể tìm thấy hằng số c = 1, và N a = 0, và miễn là N> N₀, N² sẽ luôn lớn hơn N² / 2-N / 2. Chúng ta có thể dễ dàng chứng minh điều này bằng cách trừ N² / 2 cho cả hai hàm, sau đó chúng ta có thể dễ dàng thấy N² / 2> -N / 2 là đúng khi N> 0. Do đó, chúng ta có thể đi đến kết luận rằng f (n) = O (n²), trong kiểu lựa chọn khác là " bình phương O lớn ".
Bạn có thể nhận thấy một mẹo nhỏ ở đây. Nghĩa là, nếu bạn làm cho g (n) lớn nhanh, nhanh hơn bất cứ thứ gì, O (g (n)) sẽ luôn đủ lớn. Ví dụ, đối với bất kỳ hàm đa thức nào, bạn luôn có thể đúng khi nói rằng chúng là O (2ⁿ) vì 2ⁿ cuối cùng sẽ lớn hơn bất kỳ đa thức nào.
Về mặt toán học, bạn đúng, nhưng nói chung khi chúng ta nói về Big O, chúng ta muốn biết giới hạn chặt chẽ của hàm. Bạn sẽ hiểu điều này nhiều hơn khi bạn đọc qua phần tiếp theo.
Nhưng trước khi đi, chúng ta hãy kiểm tra sự hiểu biết của bạn bằng câu hỏi sau. Câu trả lời sẽ được tìm thấy trong các phần sau nên sẽ không phải là điều cần thiết.
Câu hỏi: Một hình ảnh được biểu diễn bằng một mảng pixel 2D. Nếu bạn sử dụng vòng lặp for lồng nhau để lặp qua mọi pixel (nghĩa là bạn có vòng lặp for đi qua tất cả các cột, sau đó vòng lặp for khác bên trong để đi qua tất cả các hàng), thì độ phức tạp về thời gian của thuật toán là bao nhiêu khi hình ảnh được coi là đầu vào?
3. Chữ O lớn, chữ O nhỏ, Omega & Theta
O lớn: “f (n) là O (g (n))” iff đối với một số hằng số c và N₀, f (N) ≤ cg (N) với mọi N> N₀
Omega: “f (n) là Ω (g (n))” iff đối với một số hằng số c và N₀, f (N) ≥ cg (N) với mọi N> N₀
Theta: “f (n) là Θ (g (n))” iff f (n) là O (g (n)) và f (n) là Ω (g (n))
O nhỏ: “f (n) là o (g (n))” iff f (n) là O (g (n)) và f (n) không phải là Θ (g (n))
—Định nghĩa cơ bản về Big O, Omega, Theta và Little O
Nói một cách dễ hiểu:
- Big O (O ()) mô tả giới hạn trên của độ phức tạp.
- Omega (Ω ()) mô tả giới hạn dưới của độ phức tạp.
- Theta (Θ ()) mô tả giới hạn chính xác của độ phức tạp.
- Nhỏ O (o ()) mô tả giới hạn trên không bao gồm giới hạn chính xác .
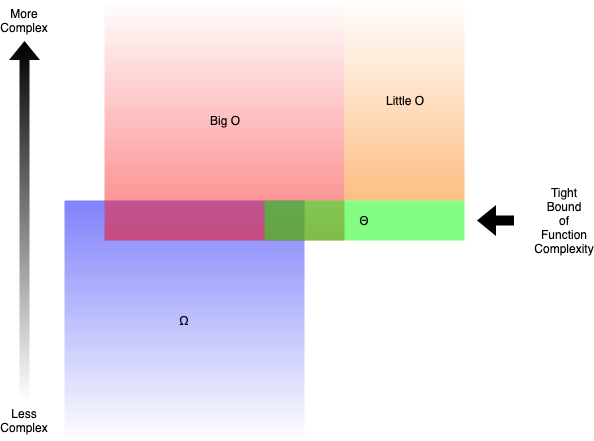
Ví dụ, hàm g (n) = n² + 3n là O (n³), o (n⁴), Θ (n²) và Ω (n). Nhưng bạn vẫn đúng nếu nói nó là Ω (n²) hoặc O (n²).
Nói chung, khi chúng ta nói về Big O, ý của chúng ta thực sự là Theta. Sẽ là vô nghĩa khi bạn đưa ra một giới hạn trên lớn hơn nhiều so với phạm vi phân tích. Điều này tương tự như việc giải các bất đẳng thức bằng cách đặt ∞ vào cạnh lớn hơn, điều này hầu như luôn khiến bạn đúng.
Nhưng làm cách nào để xác định những chức năng nào phức tạp hơn những chức năng khác? Trong phần tiếp theo bạn sẽ đọc, chúng ta sẽ tìm hiểu điều đó một cách chi tiết.
4. So sánh độ phức tạp giữa các Os lớn điển hình
Khi chúng ta đang cố gắng tìm ra Big O cho một hàm cụ thể g (n), chúng ta chỉ quan tâm đến số hạng chi phối của hàm. Thuật ngữ chiếm ưu thế là thuật ngữ phát triển nhanh nhất.
Ví dụ, n² phát triển nhanh hơn n, vì vậy nếu chúng ta có một cái gì đó như g (n) = n² + 5n + 6, nó sẽ là O (n²) lớn. Nếu bạn đã thực hiện một số phép tính trước đây, điều này rất giống với cách tìm giới hạn cho đa thức phân số, cuối cùng bạn chỉ quan tâm đến số hạng chính của tử số và mẫu số.

Nhưng chức năng nào phát triển nhanh hơn các chức năng khác? Thực ra có khá nhiều quy tắc.
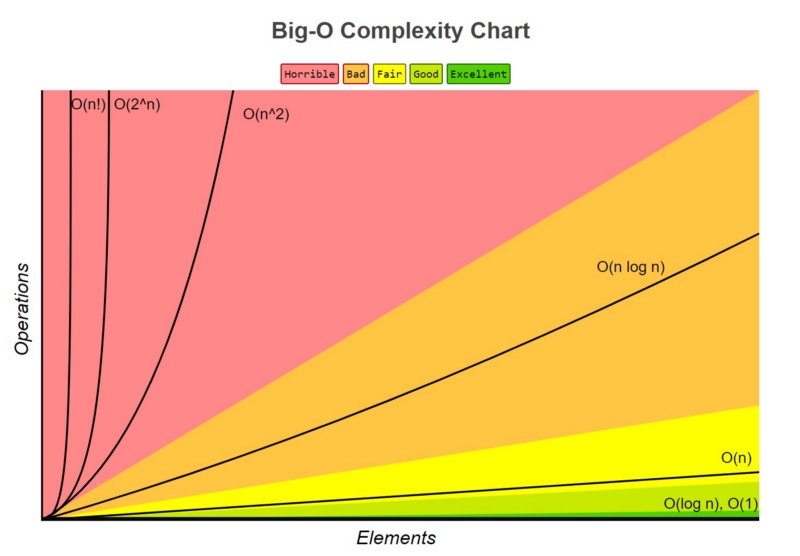
1. O (1) có độ phức tạp thấp nhất
Thường được gọi là “thời gian không đổi” , nếu bạn có thể tạo ra một thuật toán để giải quyết vấn đề trong O (1), có lẽ bạn đang ở trạng thái tốt nhất. Trong một số tình huống, độ phức tạp có thể vượt ra ngoài O (1), khi đó chúng ta có thể phân tích chúng bằng cách tìm đối chứng O (1 / g (n)) của nó. Ví dụ, O (1 / n) phức tạp hơn O (1 / n²).
2. O (log (n)) phức tạp hơn O (1), nhưng kém phức tạp hơn đa thức
Vì độ phức tạp thường liên quan đến các thuật toán chia và chinh phục, O (log (n)) nói chung là độ phức tạp tốt mà bạn có thể đạt được cho các thuật toán sắp xếp. O (log (n)) ít phức tạp hơn O (√n), vì hàm căn bậc hai có thể được coi là một đa thức, trong đó số mũ là 0,5.
3. Độ phức tạp của đa thức tăng khi số mũ tăng
Ví dụ, O (n⁵) phức tạp hơn O (n⁴). Do tính đơn giản của nó, chúng ta thực sự đã xem qua khá nhiều ví dụ về đa thức trong các phần trước.
4. Cấp số nhân có độ phức tạp lớn hơn đa thức miễn là các hệ số là bội số dương của n
O (2ⁿ) phức tạp hơn O (n⁹⁹), nhưng O (2ⁿ) thực sự ít phức tạp hơn O (1). Chúng tôi thường lấy 2 làm cơ sở cho hàm mũ và logarit vì mọi thứ có xu hướng là hệ nhị phân trong Khoa học máy tính, nhưng số mũ có thể được thay đổi bằng cách thay đổi các hệ số. Nếu không được chỉ định, cơ số cho logarit được giả định là 2.
5. Nguyên tố có độ phức tạp lớn hơn cấp số nhân
Nếu bạn quan tâm đến suy luận, hãy tra cứu hàm Gamma , nó là sự tiếp tục giải tích của một giai thừa. Một bằng chứng ngắn gọn là cả hai giai thừa và cấp số nhân đều có cùng một số phép nhân, nhưng các số được nhân tăng lên đối với các giai thừa, trong khi không đổi đối với cấp số nhân.
6. Nhân các điều khoản
Khi nhân lên, độ phức tạp sẽ lớn hơn ban đầu, nhưng không nhiều hơn tương đương với việc nhân một thứ phức tạp hơn. Ví dụ, O (n * log (n)) phức tạp hơn O (n) nhưng kém phức tạp hơn O (n²), vì O (n²) = O (n * n) và n phức tạp hơn log (n ).
Để kiểm tra sự hiểu biết của bạn, hãy thử xếp hạng các chức năng sau từ phức tạp nhất đến phức hợp cho thuê. Các giải pháp với lời giải thích chi tiết có thể được tìm thấy trong phần sau khi bạn đọc. Một số trong số chúng có nghĩa là phức tạp và có thể yêu cầu một số hiểu biết sâu hơn về toán học. Khi bạn đi đến giải pháp, bạn sẽ hiểu chúng nhiều hơn.
Câu hỏi: Xếp hạng các chức năng sau từ phức tạp nhất đến phức hợp cho thuê.
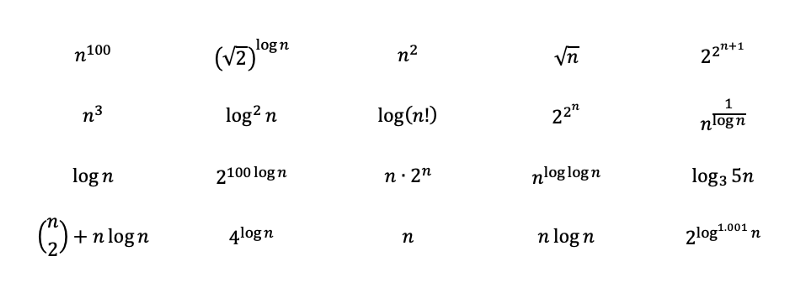
Lời giải cho Phần 2 Câu hỏi:
Nó thực sự được coi là một câu hỏi mẹo để kiểm tra sự hiểu biết của bạn. Câu hỏi cố gắng khiến bạn trả lời O (n²) vì có một vòng lặp for lồng nhau. Tuy nhiên, n được cho là kích thước đầu vào. Vì mảng hình ảnh là đầu vào và mỗi pixel chỉ được lặp lại một lần nên câu trả lời thực sự là O (n). Phần tiếp theo sẽ xem xét các ví dụ khác như thế này.
5. Sự phức tạp về thời gian và không gian
Cho đến nay, chúng ta mới chỉ thảo luận về độ phức tạp về thời gian của các thuật toán. Tức là chúng ta chỉ quan tâm đến việc chương trình mất bao nhiêu thời gian để hoàn thành nhiệm vụ. Điều quan trọng nữa là không gian chương trình có để hoàn thành nhiệm vụ. Độ phức tạp của không gian liên quan đến việc chương trình sẽ sử dụng bao nhiêu bộ nhớ, và do đó cũng là một yếu tố quan trọng cần phân tích.
Độ phức tạp không gian hoạt động tương tự như độ phức tạp thời gian. Ví dụ, sắp xếp lựa chọn có độ phức tạp không gian là O (1), bởi vì nó chỉ lưu trữ một giá trị nhỏ nhất và chỉ số của nó để so sánh, không gian tối đa được sử dụng không tăng theo kích thước đầu vào.
Một số thuật toán, chẳng hạn như sắp xếp theo nhóm, có độ phức tạp về không gian là O (n), nhưng có thể giảm độ phức tạp về thời gian thành O (1). Sắp xếp nhóm sắp xếp mảng bằng cách tạo danh sách được sắp xếp gồm tất cả các phần tử có thể có trong mảng, sau đó tăng số lượng bất cứ khi nào gặp phần tử. Cuối cùng mảng đã sắp xếp sẽ là các phần tử danh sách được sắp xếp lặp lại theo số lượng của chúng.
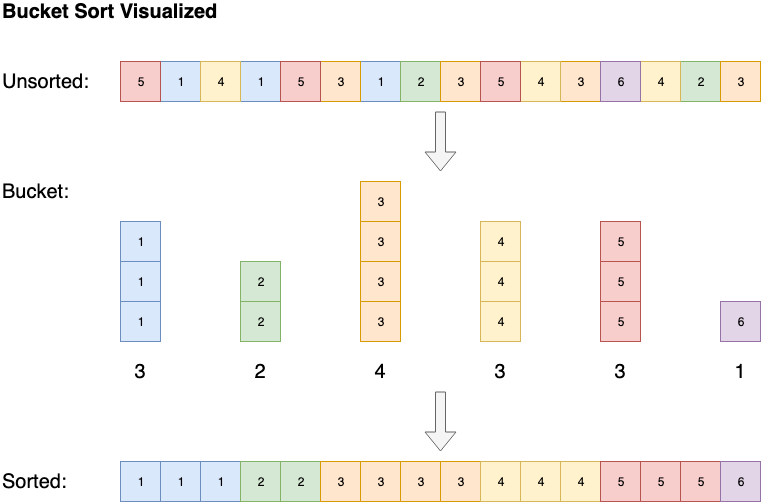
6. Tốt nhất, Trung bình, Tồi nhất, Độ phức tạp Dự kiến
Sự phức tạp cũng có thể được phân tích thành trường hợp tốt nhất, trường hợp xấu nhất, trường hợp trung bình và trường hợp dự kiến.
Ví dụ , hãy lấy phân loại chèn . Sắp xếp chèn lặp qua tất cả các phần tử trong danh sách. Nếu phần tử lớn hơn phần tử trước của nó, nó sẽ chèn phần tử đó về phía sau cho đến khi nó lớn hơn phần tử trước đó.
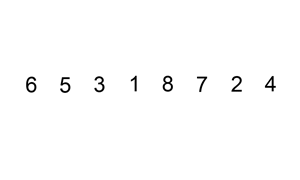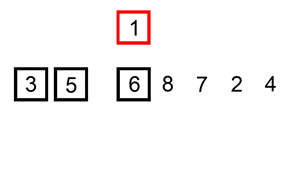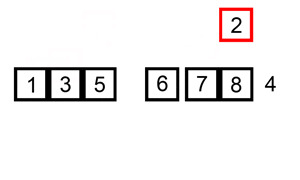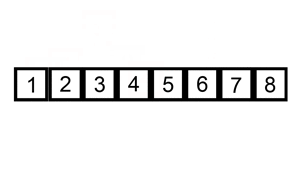
Nếu mảng được sắp xếp ban đầu, sẽ không có hoán đổi nào được thực hiện. Thuật toán sẽ chỉ lặp qua mảng một lần, dẫn đến độ phức tạp về thời gian là O (n). Do đó, chúng ta sẽ nói rằng độ phức tạp thời gian trong trường hợp tốt nhất của sắp xếp chèn là O (n). Độ phức tạp của O (n) cũng thường được gọi là độ phức tạp tuyến tính .
Đôi khi một thuật toán chỉ gặp vận rủi. Ví dụ, sắp xếp nhanh sẽ phải duyệt qua danh sách trong thời gian O (n) nếu các phần tử được sắp xếp theo thứ tự ngược lại, nhưng trung bình nó sắp xếp mảng trong thời gian O (n * log (n)). Nói chung, khi chúng tôi đánh giá độ phức tạp về thời gian của một thuật toán, chúng tôi sẽ xem xét hiệu suất trong trường hợp xấu nhất của chúng . Thông tin thêm về điều đó và sắp xếp nhanh sẽ được thảo luận trong phần tiếp theo khi bạn đọc.
Độ phức tạp trường hợp trung bình mô tả hiệu suất mong đợi của thuật toán. Đôi khi liên quan đến việc tính toán xác suất của từng tình huống. Nó có thể trở nên phức tạp để đi vào chi tiết và do đó không được thảo luận trong bài viết này. Dưới đây là bảng gian lận về độ phức tạp về thời gian và không gian của các thuật toán điển hình.
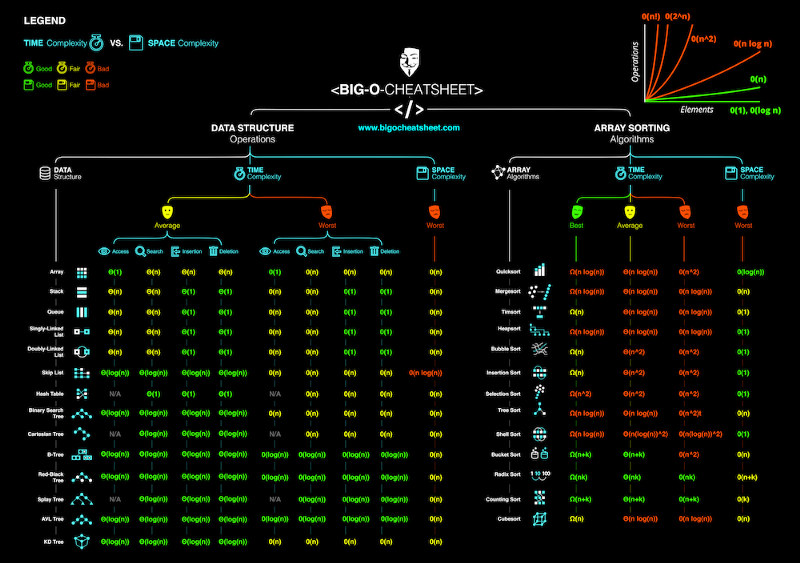
Lời giải cho Phần 4 Câu hỏi:
Bằng cách kiểm tra các hàm, chúng ta có thể ngay lập tức xếp hạng các đa thức sau từ phức tạp nhất đến phức hợp cho thuê với quy tắc 3. Trong đó căn bậc hai của n chỉ là n với lũy thừa của 0,5.
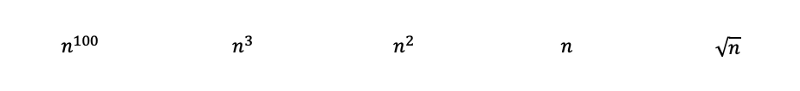
Sau đó, bằng cách áp dụng quy tắc 2 và 6, chúng ta sẽ nhận được những điều sau đây. Nhật ký cơ sở 3 có thể được chuyển đổi sang cơ sở 2 với các chuyển đổi cơ sở nhật ký . Nhật ký cơ sở 3 vẫn phát triển chậm hơn một chút so với nhật ký cơ sở 2, và do đó được xếp hạng sau.
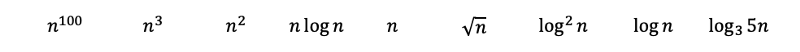
Phần còn lại có thể trông hơi phức tạp, nhưng chúng ta hãy cố gắng tiết lộ bộ mặt thật của họ và xem chúng ta có thể đặt chúng ở đâu.
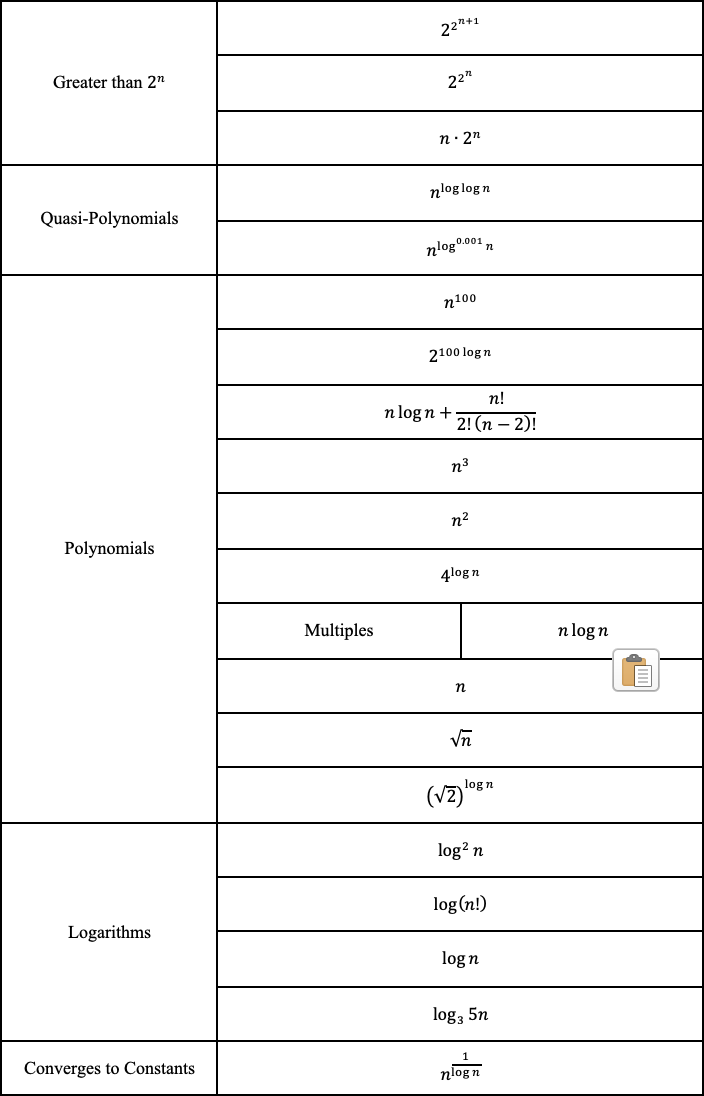
Trước hết, 2 đối với lũy thừa của 2 đối với lũy thừa của n lớn hơn 2 đối với lũy thừa của n, và +1 gia vị của nó thậm chí còn nhiều hơn.

Và vì chúng ta biết 2 thành lũy thừa của log (n) với cơ sở 2 bằng n, chúng ta có thể chuyển đổi như sau. Nhật ký với 0,001 dưới dạng số mũ phát triển nhiều hơn một chút so với hằng số, nhưng ít hơn hầu hết mọi thứ khác.

Một với n thành lũy thừa của log (log (n)) thực sự là một biến thể của bán đa thức , lớn hơn đa thức nhưng nhỏ hơn cấp số nhân. Vì log (n) phát triển chậm hơn n nên độ phức tạp của nó sẽ ít hơn một chút. Cái có log nghịch đảo hội tụ đến hằng số, vì 1 / log (n) phân kỳ đến vô cùng.

Các giai thừa có thể được biểu diễn bằng các phép nhân, và do đó có thể được chuyển đổi thành các phép cộng bên ngoài hàm logarit. "N chọn 2" có thể được chuyển đổi thành một đa thức với số hạng bậc ba là lớn nhất.

Và cuối cùng, chúng ta có thể xếp hạng các hàm từ phức tạp nhất đến ít phức tạp nhất.
Tại sao BigO không quan trọng
!!! - CẢNH BÁO - !!!
Nội dung thảo luận ở đây thường không được hầu hết các lập trình viên trên thế giới chấp nhận . Thảo luận về rủi ro của riêng bạn trong một cuộc phỏng vấn. Mọi người thực sự đã viết blog về cách họ thất bại trong các cuộc phỏng vấn trên Google vì họ đặt câu hỏi về cơ quan, như ở đây.
!!! - CẢNH BÁO - !!!
Vì trước đây chúng ta đã biết rằng độ phức tạp về thời gian trong trường hợp xấu nhất đối với sắp xếp nhanh là O (n²), nhưng O (n * log (n)) đối với sắp xếp hợp nhất, sắp xếp hợp nhất sẽ nhanh hơn - phải không? Vâng, bạn có thể đã đoán rằng câu trả lời là sai. Các thuật toán chỉ được sắp xếp theo cách giúp sắp xếp nhanh chóng “sắp xếp nhanh” .
Để chứng minh, hãy xem trang trinket.io mà tôi đã thực hiện. Nó so sánh thời gian để sắp xếp nhanh chóng và sắp xếp hợp nhất. Tôi chỉ cố gắng kiểm tra nó trên các mảng có độ dài lên đến 10000, nhưng như bạn có thể thấy cho đến nay, thời gian để hợp nhất sắp xếp tăng nhanh hơn sắp xếp nhanh. Mặc dù sắp xếp nhanh có độ phức tạp chữ thường thấp hơn là O (n²), khả năng xảy ra là thực sự thấp. Khi nói đến sự gia tăng tốc độ sắp xếp nhanh có hơn sắp xếp hợp nhất bị giới hạn bởi độ phức tạp O (n * log (n)), sắp xếp nhanh kết thúc với hiệu suất trung bình tốt hơn.
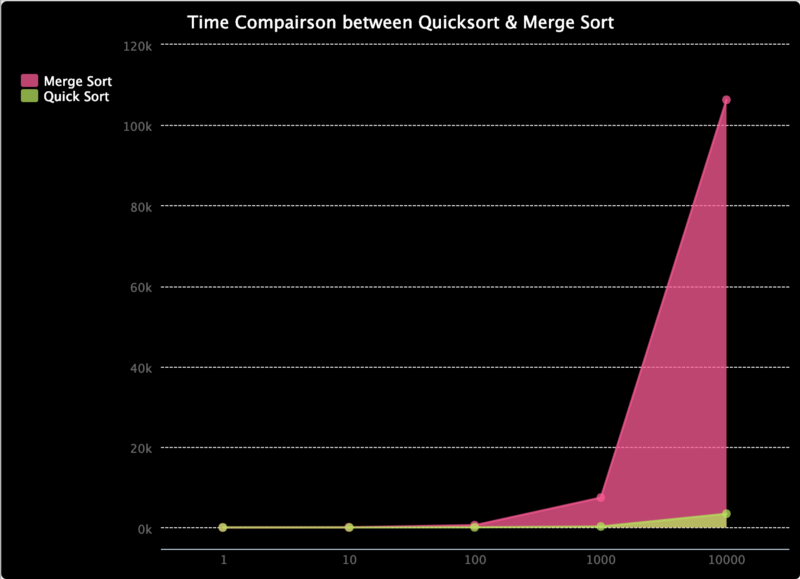
Tôi cũng đã lập biểu đồ dưới đây để so sánh tỷ lệ giữa thời gian chúng mất, vì khó có thể nhìn thấy chúng ở các giá trị thấp hơn. Và như bạn có thể thấy, phần trăm thời gian thực hiện để sắp xếp nhanh theo thứ tự giảm dần.
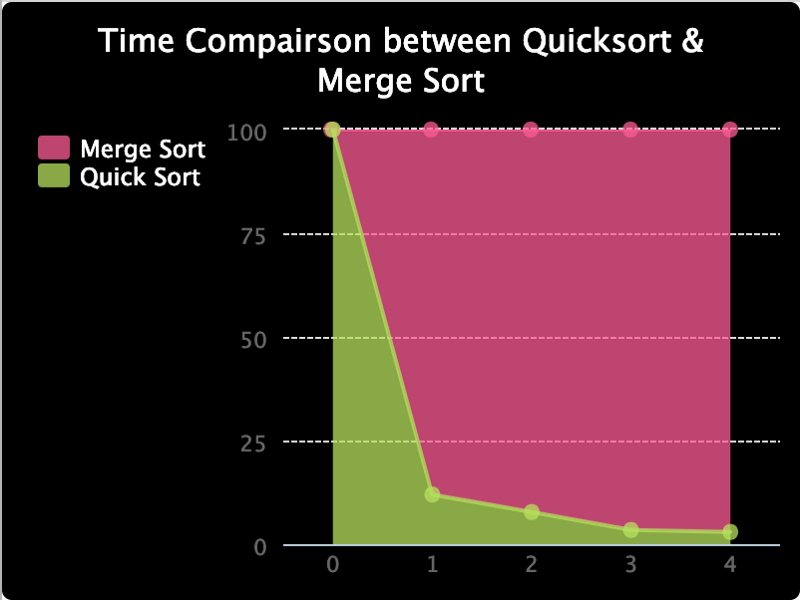
Đạo lý của câu chuyện là, ký hiệu Big O chỉ là một phân tích toán học để cung cấp tham chiếu về các tài nguyên được sử dụng bởi thuật toán. Thực tế, kết quả có thể khác. Nhưng nói chung là một thực tiễn tốt khi cố gắng giảm bớt độ phức tạp của các thuật toán của chúng tôi, cho đến khi chúng tôi gặp phải trường hợp mà chúng tôi biết mình đang làm gì.

إرسال تعليق